Math 191 Calculus
1
 |
| Brief Study Guide for
Chapter 7 |
Preview of
Chapter 7 |
| In this chapter we consider the topic of
inverse functions, introduce 22 new
functions and use l'Hopital's rule.
The 22 new functions consist of |
| |
2 logarithmic functions, |
| |
2 exponential functions, |
| |
6 inverse trigonometric functions, |
| |
6 hyperbolic functions and |
| |
6 inverse hyperbolic functions. (We actually
don't cover these last 6 functions.) |
| For each one of these functions, mathematicians
want to know about or how to do roughly a dozen things, referred herein as the The "Dozen" Aspects of New Functions |
| As you are introduced to each of the 16 functions
that we consider, analyze it against the list above. |
|
Calculus
1 Lesson 7.1
Inverse Functions |
| The following topics are the most
important. Typical exercises from Calculus, 4th edition, by James Stewart, are
assigned at the end of each objective. |
| 1. |
Do the following symbolically, numerically
and
graphically where applicable: Given a function f over a domain, |
| a. |
determine whether it is one-to-one;
P391#3,5,7,9,11,15 |
| b. |
find its inverse, g (or f -1), if it
exists; P391#25,27,29,31,33 |
| c. |
give the domain and range of f and g;
P392#35,37 |
| d. |
find the derivative of f and g and the
connection between them; P392#39,41 |
| e. |
give the equation of the line tangent to the
functions f and g at corresponding places; |
| f. |
graph the function f and its inverse g on the
same set of axes. P392#35,37 |
|
Calculus
1 Lesson 7.2*
Natural Logarithms
Note: Sections 7.2*, 7.3* and 7.4* are
printed on the gray pages of Stewart following sections 7.2, 7.3 and 7.4. |
| 1. |
Define the natural logarithm function. Text |
| 2. |
Analyze the graph of f(x) = ln x using f, f ',
and f ''. Text |
| 3. |
Use algebraic properties of ln x.
P428#1,3,5,7 |
| 4. |
Graph expressions involving ln x without a
calculator. P428#9,11 |
| 5. |
Differentiate functions involving ln x
including implicit differentiation. P428#13,15,21,25,27 |
| 6. |
Give the equation of the tangent line of a
function involving ln x. P428#41 |
| 7. |
Evaluate integrals involving the natural
logarithm. P429#59,61,65 |
| 8. |
Use logarithmic differentiation.
P429#55,57 |
| Maple Assignment:
none |
|
Calculus
1 Lesson 7.3*
Natural Exponentials
Note: Sections 7.2*, 7.3* and 7.4* are
printed on the gray pages of Stewart following sections 7.2, 7.3 and 7.4. |
| 1. |
Give the definition of natural exponentiation. Text |
| 2. |
Solve equations involving natural exponential and logarithmic
expressions. P435#3,5,7,9 |
| 3. |
Graph expressions involving ex without a
calculator. P435#17,21 |
| 4. |
Differentiate functions involving exponential and logarithmic
functions including the chain rule and implicit differentiation. P435#29-41 odd |
| 5. |
Give the equation of the tangent line of a function involving
ex. P435#43 |
| 6. |
Solve word problems involving logarithms and exponentials.
P436#53,55 |
| 7. |
Analyze the bell shaped curve from statistics.
P436#66 |
| 8. |
Integrate expressions involving the natural
exponential function. P436#67,69,71,73 |
| Maple Assignment:
See Maple Assignment |
|
Calculus
1 Lesson 7.4* General
Exponentials and Logs
Note: Sections 7.2*, 7.3* and 7.4*
are printed on the gray pages of Stewart following sections 7.2, 7.3 and 7.4. |
| 1. |
For the general exponential and logarithm
functions, do all of the following: |
| 1.a |
define them; Text |
| 1.b. |
evaluate; P445#7,13 |
| 1.c |
graph; P445#11,12,15 |
| 1.d |
finds limits; P445#21,22 |
| 1.e |
differentiate using chain rule;
P445#23-35 odd |
| 1.f |
integrate; P446#41,42,43,44 |
| 2. |
Compare the growth of the power function versus
the exponential function. P445#19 |
| 3. |
Find the equation of the tangent line of a curve
involving logarithms and exponentials. P445#39 |
| 4. |
Find the area under the curve involving logarithms
and exponentials. P446#43 |
| 5. |
Give an overview of the development of logarithm
and exponential functions. Text: sections 7.2*-7.4* |
| Maple Assignment:
none |
|
Calculus
1 Lesson 7.6
Inverse Trigonometric Functions |
| 1. |
For the inverse trig functions, do
all of the following: |
| 1.a |
define; Text |
| 1.b. |
evaluate; P461#1,5,11 |
| 1.c |
graph; P461#15 |
| 1.d |
finds limits; P461#45 |
| 1.e |
differentiate using chain rule;
P461#23-33 odd |
| 1.f |
integrate; P462#59-67 |
| 2. |
Derive the formula for the
derivative of an inverse trig function.
(sin-1, cos-1 or tan-1) . P461#19 |
| 3. |
Find the equation of the tangent
line of a curve involving inverse trig functions. P461#40 |
| 4. |
Find the area under the curve
involving inverse trig functions. P462#73 |
| 5. |
Solve a related rates word problem
involving inverse trig functions. P462#49 |
| Maple Assignment:
Combined with section 7.6 maple worksheet. |
|
Calculus
1 Lesson 7.7
Hyperbolic Functions |
| 1. |
For the hyperbolic functions, do all of the following: |
| 1.a |
define; Text |
| 1.b. |
evaluate; P468#1,3 |
| 1.c |
graph; P469#22 |
| 1.d |
finds limits; P469#23a,e |
| 1.e |
differentiate using chain rule;
P469#31,37,43,47 |
| 1.f |
integrate; P470#55,56,59,61 |
| 2. |
Derive the formula for the derivative of a
hyperbolic function. P469#24a,b |
| 3. |
Find the equation of the tangent line of a curve
involving hyperbolic functions. (no specific examples in text)P470#53 |
| 4. |
Find the area under the curve involving hyperbolic
functions. (no specific examples in text) |
| 5. |
Solve a catenary word problem
P469#49 |
| 6. |
Explain why trig functions are often called
circular functions and hyperbolic functions are so named. |
| Maple Assignment: See
Maple Assignment |
|
Calculus
1 Lesson 7.8
l'H˘pital's Rule |
| 1. |
Name the seven indeterminate forms. Text |
| |
P470-478 |
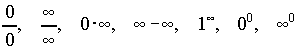 |
These indeterminate forms are discussed. |
| 2. |
Determine whether l'H˘pital's rule applies and,
if so, apply it to find limits of the seven indeterminate forms. P478#5-61 every other
odd. |
|
| |

