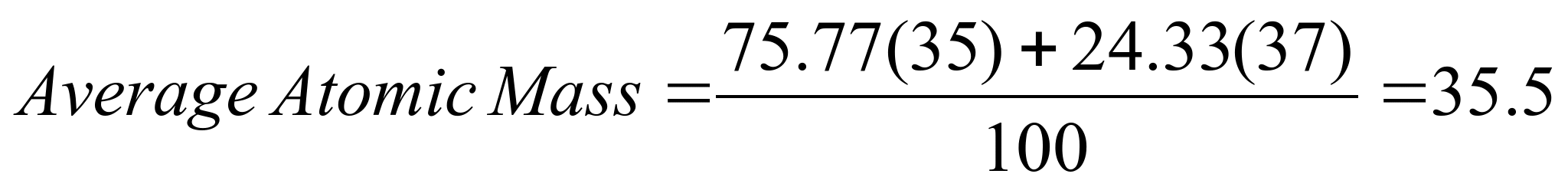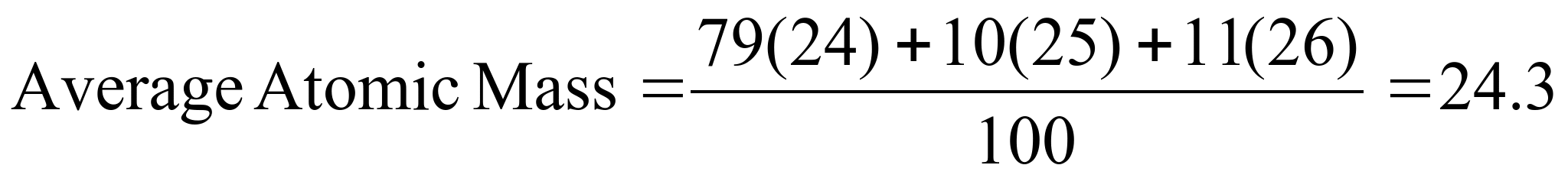Answers

1. 8 + 6 = 14 particles

2. 8 particles with mass of 9 = 8*9 = 72

6 particles with mass of 7 = 6* 7 = 42

Total mass = 72+ 42 = 114

3. Average = Total mass/number of particles

Average mass = 114/14 = 8.1

Notice: none of the particles has this exact mass, but that is the average mass of a particle across the whole sample.

How does this translate into average atomic mass calculations? Recall that for each element there may be different isotopes of the element that exist.

Isotope : atoms of the same element that have different numbers of neutrons.

Recall, that if the atoms are the same element, they must have the same number of protons. However, if you change the number of neutrons in an atom, you necessarily change the mass of that atom.

For example, one isotope of chlorine is Cl-35 and one isotope is Chlorine-37. Chlorine-35 has a mass of 35 amu, which comes from 17 protons and 18 neutrons. Chlorine-37 has a mass of 37 amu, which comes from 17 protons and 20 neutrons.

If you have a measurable sample of chlorine, you will have a huge number of chlorine atoms, some will be chlorine-35 and some will be chlorine-37. However, in all likelihood, you will not be dealing with this sample of particles one atom at a time, you will be dealing with the whole group. You don’t want to measure the mass of each particle individually, so you need to calculate the average atomic mass.

However, we need some information. We have the masses of the two types of particles but we need to know how many of each kind there are. That is where data about the natural abundance comes in handy.

Natural Abundance: The number of atoms of a particular isotope that are found in materials in nature. This number is frequently expressed as a percent.

For example, for Chlorine the natural abundances of the two isotopes are as follows:

Cl-35 : 75.78% and Cl-37: 24.33% (Approximately a 3:1 ratio)

We could represent this as follows:

1. Total number of particles = 8

2. Total mass = 6(35) +2(37) = 284

3. Average mass = 284/8 = 35.5

But what if we had a much larger sample, with millions of atoms. We wouldn’t want to count out them out to do the calculation.

Instead, we can use the percentages to count atoms. If we use percents as our way of counting atoms, the average atomic mass formula becomes:

Average Atomic mass =

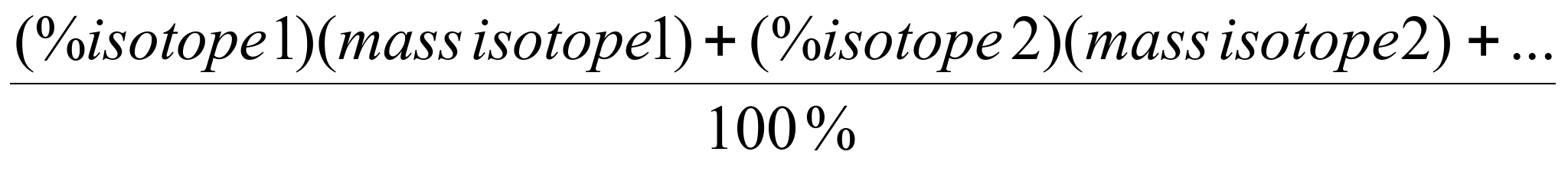
Notice: This is just like the example above. The total mass is the percent of each particle (our count of how many) * the mass of the particle.

Since we are counting particles in percent, the total number of particles is 100%.

Example 1: Determine the average atomic mass of chlorine using the above formula.

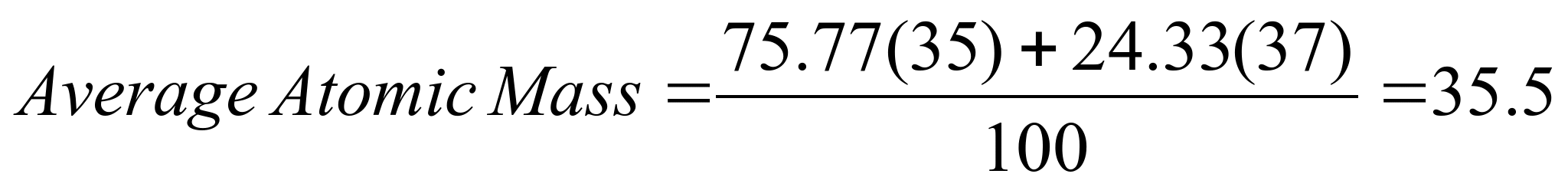
Notice, this is the same number as we calculated above, and closely agrees with the average mass for Cl found on the periodic table.

Example 2: There are 3 naturally occurring isotopes of magnesium. The relative abundance of each is shown in the table below. Using this information, determine the average atomic mass.

Isotope	Mass	% Natural Abundance
Mg- 24	24	79
Mg-25	25	10
Mg-26	26	11

To find the average atomic mass you would calculate:

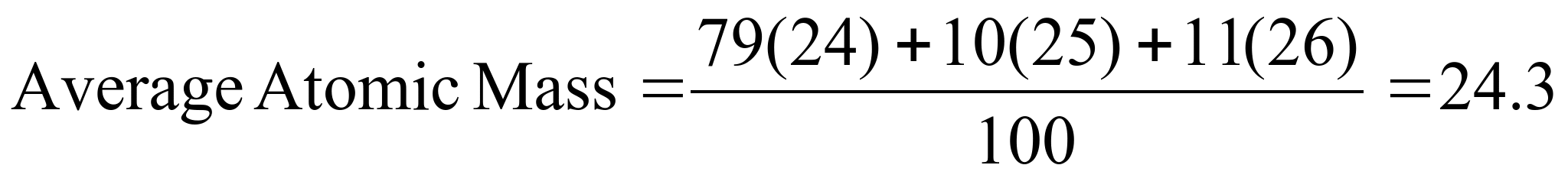
This is in agreement with the average atomic mass for Mg seen on the periodic table.

Example 3: Nickel (Ni) has an average atomic mass of 58.69. Use this information to determine the naturally occurring isotopes of nickel.

Answer: You cannot do this! There is no way to know what the naturally occurring elements of nickel are except to take samples of nickel and test them (or look at the results of a test someone else has completed). When you do so, you find that there are 5 naturally occurring isotopes of nickel, with the following relative abundances:

Isotope	Mass	% Natural Abundance
Ni-58	58	68.3
Ni-59	59	0
Ni-60	60	26.1
Ni-61	61	1.13
Ni-62	62	3.59
Ni-63	63	0
Ni-64	64	0.91

Again, we cannot fill in the above table just based on the periodic table.

The most abundant isotope is Ni-58. Nickel has an atomic number of 28, which means it always has 28 protons. Therefore, Ni-58 must have 30 neutrons.