Ideal Gas Law
Read Section 5.3 of the textbook.
The Ideal Gas Law can be thought of as a combination of Avagadro's Law and the Combined Gas Law. Avagadro's Law states that equal volumes of gases at the same temperature and pressure contain the same number of molecules (or moles of molecules).
Mathematically this can be stated as V = constant · n,
or V1 / n1 = V2 / n2,
where n = # of moles.
The Combined Gas Law is P1V1 / T1 = P2V2 / T2.
Putting the two laws together yields P1V1 / (n1T1) = P2V2 / (n2T2).
This means that PV / nT equals a constant, which is represented by R. This constant is evaluated using this experimental data: One mole of any gas at STP occupies 22.4 L. So,
| P = 1.00 atm | V = 22.4 L |
| n = 1.00 mole | T = 273 K |
| constant = R = ? | |
R = PV / (nT)
![]()
R = 0.0821 L atm/(mole K)
R is called the universal gas constant. It is true for any gas. The equation is usually written
PV = nRT, and this is called the Ideal Gas Law. It is true for any gas, within certain limits that we will discuss later.
R is a constant, but it may be written using different units - and so the numerical value changes accordingly. For example, if we choose to have R in terms of torr, we multiply the above value by 760 torr / atm. Write this out on paper, verify that the unit of atm cancels and that the answer is R = 62.4 L torr / (moleK).
Example 1) A cylinder contains 2000.0 mL of O2 gas at 1500.0 psi and 25°C. How many moles of O2 gas are in the cylinder? What is the mass of O2 gas in the cylinder?
| V = 2000.0 mL | P = 1500.0 psi | T = 25°C + 273 = 298 K |
| gas is O2 | n = ? | m = ? |
PV = nRT, so
n = PV /(RT)
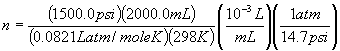
n = 8.34 mole
To convert moles to mass we use the molar mass of O2, as we learned in Chapter 3:
8.34 mole x 32.0 g/mole = 267 g
************************
There are several different forms of the Ideal Gas Law that are important. In
these forms the way to calculate n, the number of moles, has been re-expressed.
On paper, verify for yourself using dimensional analysis that number of moles is
calculated by dividing the mass of a sample by its molar mass. Symbolically this
is n = m / M, where m = mass of sample and M = molar mass. Substituting this
expression into the Ideal Gas Law gives PV = mRT/M.
Then, dividing both side by V and regrouping:
![]()
Notice that m/V is density, D. So,
P = DRT/M, where M is the molar mass of the gas.
Example 2) Calculate the density of N2 gas at 1.00 atm and 25°C.
| P = 1.00 atm | T = 25°C + 273 = 298 K |
| gas is N2 | M = 28.0 g/mole |
| D = ? | |
Use the Ideal Gas Law in the form P = DRT/M, but rearrange to solve for D.
D = PM / (RT)
Substitute in the values, and verify both the units & numerical value of the answer.
D = 1.14 g/L